Rope selection
A boat is anchored at a wharf in accordance with the figure below. Which of the following three hawser (rope) selections will make the boat endure a storm that generates a 50 kN tensile load to the prow hawser.
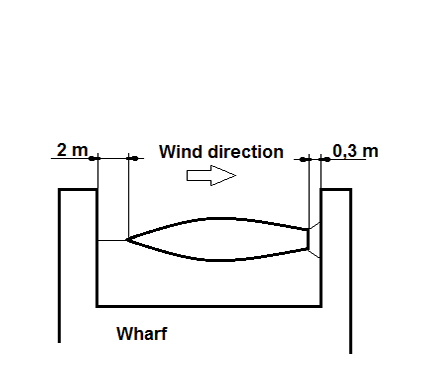
© Anders Persson, Borås
Consider the following three options:
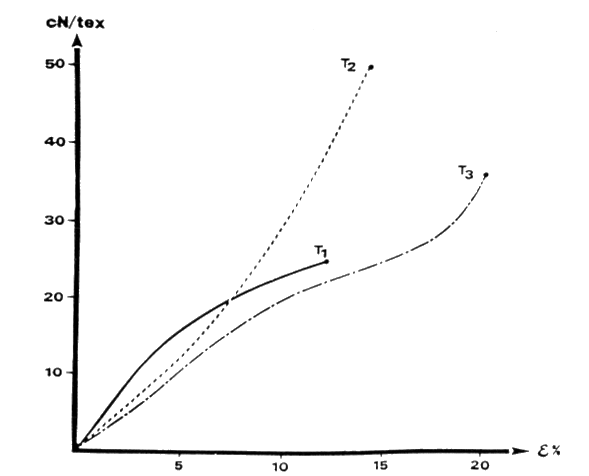
T1 = 160 ktex, T2 = 120 ktex, T3 = 190 ktex, with tensile curves as:
Condition 1: the boat must not hit the rear wharf, i.e. the prow hawser must not elongate more than 0.3 m, which is equivalent to 0.3 m/ 2 m = 15 % strain.
Condition 2: the prow hawser must not break, meaning that the normal stress of the prow hawser must not exceed its tenacity, which are the ultimate stress of the individual graphs.
Analyse each one of the three options.
T1
According to the graph the strain at break of T1 is below the 15%. Hence, it will not elongate to the extent that the rear hits the wharf. C1 – check! Will T1 endure the 50 kN? The graph tells that T1 has a tenacity of 25 cN/tex and the linear density of T1 is 160 ktex meaning that its ultimate load is 25·102 · 160·103 N = 40 kN, which is below the force generated by the storm. Thus, T1 will break. C2 – not fulfilled!
T2
According to the graph the strain at break of T2 is close to 15%. There is a risk that it may elongate too much. How about the strength? The graph tells that a 50 cN/tex tenacity and its 120 ktex linear density gives it an ultimate load of 60 kN which is higher than the 50 kN from the storm. Hence, once it faces the 50 kN it will not reach its ultimate strain and both C1 & C2 are fulfilled.
T3
According to the graph it is much tougher than the 15% and has a tenacity of about 37 cN/tex, which gives an ultimate load of 37·102 · 190·103 N = 70.3 kN. The hawser will not break but how long will it elongate at 50 kN load? The graph suggests that 15% strain generates a 25 cN/tex stress in T3, which is equivalent to 25·102 · 190·103 N = 47.5 kN. Thus the hawser will elongate more than 0.3 m once applied to 50 kN.
-
Project
Contact
This resource was developed as part of an Erasmus+ project, funded with support from the European Commission under grant agreement 2016-1-SE01-KA203-22064.
The project was a collaboration between:
- The University of Borås, Sweden
- The University of the Highlands and Islands, Scotland
- The University of Alcalá, Spain
- Digital Connections, Scotland
This resource has been released under Creative Commons license CC-BY-SA 4.0.
Disclaimer
If you would like more information on this resource please contact:
- Academic content – The University of Boras (www.hb.se)
- Technical resource development – The University of the Highlands and Islands Educational Development Unit - EDU (edu@uhi.ac.uk)
Except where otherwise noted, this website is licensed under Creative Commons license CC-BY-SA 4.0. All images used under permission remain the copyright of the license holder.
Download a copy of this resource in PDF format.
You can also print individual pages by printing directly from the browser.
-
