Crystallinity and semicrystalline polymers

The driving force behind crystallization is best explained in a thermodynamic context. A polymer will crystallize in case it can form sufficiently strong and frequent intermolecular attractions to compensate for the loss in disorder in the phase transition from disordered to ordered. It is a primary phase transition going from liquid to solid. The change in Gibbs free energy, ∆G, is expressed as:

The heat of crystallization, ∆H, which is exothermal, thereby renders a negative value. Also the change of ∆S, where S is a measure of the systems disorder, is negative since crystallization makes the system less disordered. Hence, ∆H has to compensate for the loss of ∆S at a certain crystallization temperature in order to reduce Gibbs free energy. The lower the crystallization temperature, T, the smaller the term -T∆S becomes and the potential to reduce Gibbs energy increases. During heating melting of the crystalline structure will occur at a temperature where ∆G equals zero. This constitutes its melting temperature T_m = ∆H/∆S. For polymers with strong and dense intermolecular attraction or for polymers that are rather rigid, thereby do not lose quite as much disorder during their transition they get high T_m’s. For rigid polymers that form strong and dense intermolecular attraction the T_m becomes very high; typical of high performance polymers. It is also that there is a substantial margin between the T_m and T_g to enable the necessary polymer diffusion for crystallization to take place. As a rule of thumb the highest crystallization rate is accomplished right between the T_m and T_g, i.e. (T_m+T_g)/2.

A crystalline structure can be described by an ordered 3D structure where, in this case the polymer has arranged itself. The smallest common denominator can be described as a unit cell usually in the form of a cubic, rhombic or distorted rhombic configuration. They take on the configuration that enables the most intermolecular bonds. This may be associated with all-trans or perhaps a helix- conformation. Depending on the degree of supercooling and the cooling-rate during crystallization they will form lamellas of varying folding length. As illustrated in Figure 8 the ordered sequences are linked to amorphous sequences. A polymer can never be completely crystalline, hence they are called semicrystalline. Since the polymer may start to crystallize at more than one spot at once, their diffusion will be restricted.

Polymer crystallization (YouTube, 0:16)

Even if very high degree of crystallinity can be accomplished upon precipitation of a polymer solution they always contain end groups that affect the crystallization. This is also the case upon crystallization from the molten state. Hence, polymers with a lot of end-groups, which is found for low molar mass linear and for branched polymers renders low degree of crystallinity.  Also in cases of very high molar mass polymers the number of entanglements will reduce polymer diffusion needed to accomplish high the degree of crystallinity. Hence there is an optimum in terms of molar mass and thermal history for each polymer.

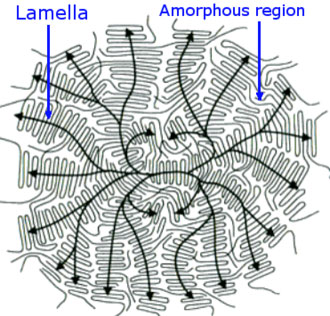
Figure 8. A schematic spherulite of a semicrystalline polymer. Arrows indicate where it was nucleated and how it grew.
Materialscientist at Wikimedia / CC BY-SA 3.0