Central limit theorem
The Central limit theorem states that the sum of a sufficiently large number of independent random variables tends toward a Normal random variable, independently of the distributions of the random variables which are added. A consequence of this theorem is this: the sample mean (normalized sum of realizations of a random variable) is another random variable, which probability density function tends to be Gaussian if the number or samples is large enough.
A condition to this theorem is that the variance of the added independent random variables must tend to infinity when this number also tends to infinity.
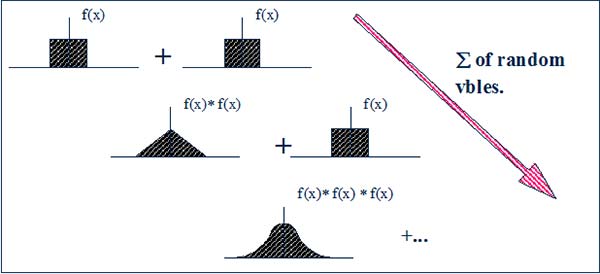
Figure 5 Probability density function of the sum of independent uniform random variables
-
Project
Contact
This resource was developed as part of an Erasmus+ project, funded with support from the European Commission under grant agreement 2016-1-SE01-KA203-22064.
The project was a collaboration between:
- The University of Borås, Sweden
- The University of the Highlands and Islands, Scotland
- The University of Alcalá, Spain
- Digital Connections, Scotland
This resource has been released under Creative Commons license CC-BY-SA 4.0.
Disclaimer
If you would like more information on this resource please contact:
- Academic content – The University of Alcalá (www.uah.es/en/)
- Technical resource development – The University of the Highlands and Islands Educational Development Unit - EDU (edu@uhi.ac.uk)
Except where otherwise noted, this website is licensed under Creative Commons license CC-BY-SA 4.0. All images used under permission remain the copyright of the license holder.
Download a copy of this resource in PDF format.
You can also print individual pages by printing directly from the browser.
-
