Ergodicity

Characterization of random signals is very important in telecommunication. The available information is usually scarce, limited to one random sample or realization of the random process or random signal.

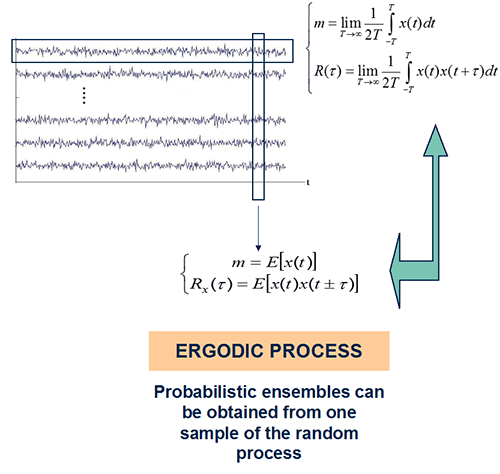
A Stochastic Process or Random Signal is said to be an Ergodic Process if its statistical properties can be deduced from a single, sufficiently long, random sample of the process (realization). In these signals it is possible to substitute the ensemble averages with averages in time. The averages calculated in the time domain with one random sample of the process are constant (mean, variance, etc), therefore only Stationary Processes can be Ergodic:

ERGODICITY $\Rightarrow$ STATIONARITY

Averages in time:
The “sample mean” of continuous-time x(t) and discrete-time x[n] signals, respectively, are given by:

${<n_{x}>}_{T} = \frac{1}{T} \int_{- \frac{T}{2}}^{\frac{T}{2}} X (t) d t$

${<n_{x}>}_{N} = \frac{1}{2 N + 1} \sum_{n = - N}^{N} X [n]$
The “sample variance” of continuous-time x(t) and discrete-time x[n] signals, respectively, are given by:

${<σ_{X}^{2}>}_{T} = \frac{1}{T} \int_{- \frac{T}{2}}^{\frac{T}{2}} (X (t) - (μ_{X})_{T})^{2} d t$

${<σ_{X}^{2}>}_{N} = \frac{1}{2 N + 1} \sum_{n = - N}^{N} (X [n] - {<μ_{X}>}_{N})^{2}$

The sample mean and sample variance of a random signal are random variables, because their values depend on the particular sample function over which they are calculated.
The time-averaged sample Autocorrelation Function (ACF) of continuous-time x(t) and discrete-time x[n] signals, respectively, are given by:

${<R_{X X}>}_{T} = \frac{1}{T} \int_{- \frac{T}{2}}^{\frac{T}{2}} X (t) X^{*} (t + τ) d t$

${<R_{X X}>}_{N} = \frac{1}{2 N + 1} \sum_{n = - N}^{N} X [n] X^{*} [n + m]$