Random signals (Stochastic processes)

A random signal (also known as Stochastic Process) is a function of one or more deterministic variables (usually time, in communications), and one or more random variables:

$X (t, ω)$ where t is a deterministic variable, and $ω$ is a random variable.

Interpretation:

For fix $ω$ : it is a time function known as “sample” or “realization”.
For fix t: it is a function of random variable.
For fix t and $ω$ : it is just a number.

The random signal is characterized with the Cumulative Distribution Function and the first order Probability Density Function:

F_{x} (x, t) = P [X (t) \leq x]

p_{x} (x, t) = \frac{\partial F_{x} (x, t)}{\partial x}

The moments of a random signal are functions of the deterministic variable. For example, if the deterministic variable is time, the mean is a time function.

η (t) = E [X (t)] = \int_{- \infty}^{\infty} x \cdot p_{x} (x, t) d x

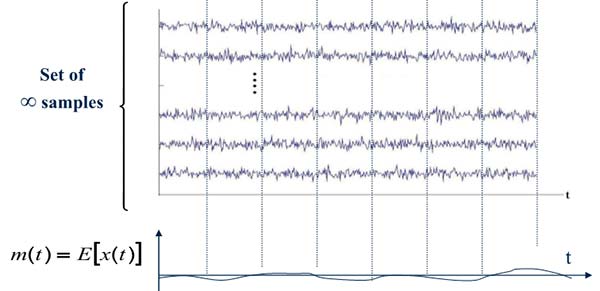
Figure 6 Illustration of random signal meaning

For the complete statistical characterization of random signals, the relationships among random variables obtained particularizing the random signals at different time instant is needed. As the number of random variables can be infinite, the complete characterization can be impossible. The relationship between pairs of random variables is usually studied, to obtain more information about the random signal properties, with the second order cumulative distribution function and the second order probability density function:

F_{X} (x_{1}, x_{2}, t_{1}, t_{2}) = P [X (t_{1}) \leq x_{1}; X (t_{2}) \leq x_{2}]

p_{x} (x_{1}, x_{2}, t_{1}, t_{2}) = \frac{\partial F_{x} (x_{1,} x_{2}, t_{1}, t_{2})}{\partial x_{1} \partial x_{2}}

These are the joint cumulative distribution function and the joint probability density function of two random variables, result of the particularization of the random signal in two time instants. Generally, these functions depends on the time instants.

Review of Basic Concepts of Probability

Random signals (Stochastic processes)