Joint characterization of two random variables

Two random variables can be jointly characterized using the 'Joint Probability Density Function' or the 'Joint Cumulative Distribution Function', defined as follows:

F_{x y} (x, y) = P (X \leq x, Y \leq y)

p_{x y} (x, y) = \frac{\partial F_{x y} (x, y)}{\partial x \partial y}

If the two variables are independent, the joint PDF is the product of marginal probability density functions:

p_{x y} (x, y) = p_{x} (x) p_{y} (y)

This reasoning can be extended to sets of `n’ random variables, concluding that the joint PDF of a set of random variables is the product of the marginal probability density functions.

p_{z} (z) = p (x_{1}, x_{2}, . . ., x_{n}) = \prod_{i = 1}^{n} p (x_{i})

Example: Find the PDF of the random variable resulting from the sum of two independent random variables, if the marginal PDF of the variables are known.

Z = X + Y

This is applied to the characterization of noise which results from adding two different kind of interferences. The objective is to find the PDF of random variable z, as a function of the PDFs of the random variables x and y.

The procedure to be applied consists in finding the cumulative distribution function of z:

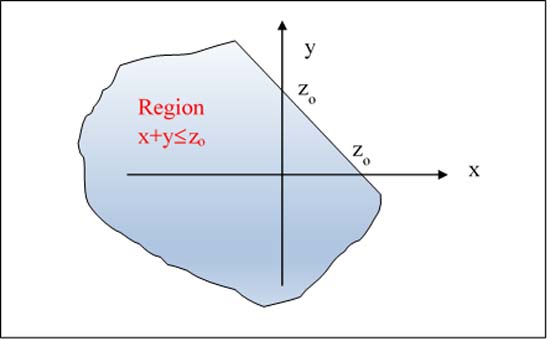
Figure 4 Graphical representation of integration area to find the CDF of the sum of two random variables

F_{z} (z_{0}) = P (z \leq z_{0}) = \int_{- \infty}^{\infty} \int_{- \infty}^{z_{0} - y} p_{x y} (x, y) d x d y

If both random variables are independent: $p_{x y} (x, y) = p_{x} (x) p_{y} (y)$

F_{z} (z_{0}) = \int_{- \infty}^{\infty} p_{y} (y) \int_{- \infty}^{z_{0} - y} p_{x} (x) d x d y

p_{z} (z_{0}) = \frac{d F_{z} (z_{0})}{d z_{0}} \int_{- \infty}^{\infty} p_{y} (y) p_{x} (z_{0} - y) d y

The PDF of the sum of two independent random variables is equal to the CONVOLUTION of the marginal PDFs. An important consequence is the fact that the sum of normal or Gaussian random variables is always Gaussian, since the convolution of Gaussian functions is also Gaussian.

An important question arises: Why don’t we use the Fourier transform, so that the Fourier transform of the desired PDF is obtained as the product of the marginal PDFs Fourier transforms?

Characteristic Function: It is defined as the Fourier transform of the probability density function.

c_{x} (f) = E \{e^{j 2 πfx}\} = \int_{- \infty}^{\infty} p_{x} (x) e^{j 2 πfx} d x

Review of Basic Concepts of Probability

Joint characterization of two random variables